じょう乱の移動計算の基礎知識

今回は、じょう乱（低気圧・トラフ）の移動速度・方向の問題を解くための基礎知識をまとめていきます。

後半では頻出パターンの問題にチャレンジしましょう。

 

基礎知識

距離・速度の単位の定義

気象では距離の単位に海里（NM）、速度の単位にノット（kt）を用います。定義が大切なので、しっかりと覚えましょう。

距離の単位：　海里

海里（NM：Nautical Mile）は、次のように定義されます。

 

緯度1/60度分です（これを１分といいます）。緯度１度ではありません。緯度1/60度分です。
いま、この場で覚えてしまいましょう。

ちなみに、経度線に沿った緯度０度から９０度までの距離は１万（km）ですから、緯度１度の距離は１万（km）÷90＝111.11（km）です。
（注）北極から赤道までの子午線の距離は１万（km）と定義されています。

したがって、緯度１/60度の距離は111.11/60＝1.852（km）となります。「１海里に、ひとはごにん（人は五人）」と覚えると便利です。

 

速度の単位：　ノット

ノット（kt：knot）は、次のように定義されます。

 

次の関係式が成り立つことを確認してください。

１（kt）＝１（NM/h）＝1/60（度/h）

 

移動距離＝速度×時間

この式は皆さんもご存知だと思います。これを使った計算問題がよく出題されるので、確認しておきましょう。

移動距離と時間から速度を求める

日常使い慣れている速度は時速（km/h）や秒速（m/s）ですね。

気象の速度の単位はノット（kt）なので、移動距離は度で表すことになります。

移動距離（度）を時間（h）で割ると、単位は（度/h）になります。

これをノット換算するのには、先に確認した「１（kt）＝1/60（度/h）」を用います。

 

例１）12時間で緯度5度進むときの速度は？

まず、距離÷時間を計算すると、5（度）÷12（h）＝5/12（度/h）です。

これをノット換算するには、1/60で割ります（＝60をかけると同じ）。

5/12（度/h）÷（1/60）（度/h/kt）＝25（kt）

 

例２）24時間で緯度10度進むときの速度は？

例１に倣って計算します。

10/24（度/h）÷（1/60）（度/h/kt）＝25（kt）

ということで、例１と同じになります（当たり前ですね）。

 

速度と時間から移動距離を求める

移動距離＝速度×時間です。

この問題では、距離の単位が「度」なのか「km（m）」なのかに注意します。

例３）低気圧が10（kt）で3時間進むと、移動距離は何度か？

10（kt）×3(h)＝10（NM/h）×3（h）＝30（NM）

１（NM）は定義により緯度1/60度の距離ですから、30（NM）を度に換算するには1/60をかけます。

30（NM）×1/60（度/NM）＝0.5（度）

 

例４）低気圧が10（kt）で3時間進むと、移動距離は何キロか？

１（度）は111.11（km）ですから、例３の結果を用いると、

0.5（度）×111.11（km/度）＝55.6（km）

となります。

 

方位

じょう乱の移動方向を聞かれることがありますので、方位について理解しておきましょう。

 

８方位

北、北西、西、南西、南、南東、東、北東　の８通りです。

 

１６方位

北、北北西、北西、西北西、西、西南西、南西、南南西、南、南南東、南東、東南東、東、東北東、北東、北北東　の１６通りです。

 

８方位と１６方位で混乱したら・・・

８方位って「北西」のような２文字なのか、あるいは「北北西」のような３文字なのか、私はよく混乱します。こんなとき、次のようなやり方で８方位を確認できます。

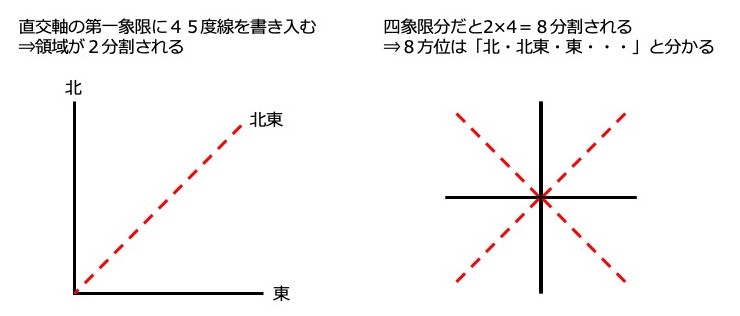
北と東をイメージした直交軸を描き、だいたい４５度のところに斜めに線を描きます。これを第一象限とすると、この象限は４５度線を描き入れることで２分割されました（図１）。

ということは、四象限では２×４＝８分割されることになります。これで「８方位」と認識することができました。

 

 

問題を解いてみよう

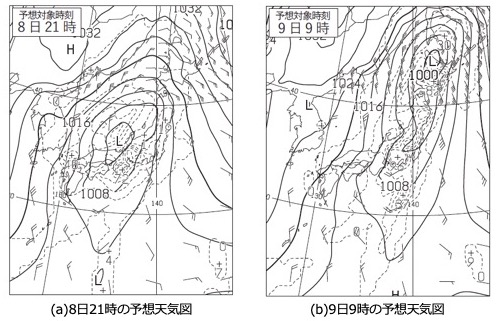
では実際の出題で作業手順を確認してみましょう（55-1-2(1)①）。

 

 

じょう乱の移動の速さを求める

速さは移動距離÷移動時間で求めます。

移動距離の測定は、１）図面上でじょう乱の移動距離（mm）を測る、２）経度線を使って移動距離（mm）を「度」に変換する、の２段階からなります。

１）図面上でじょう乱の移動距離（mm）を測る

天気図上でじょう乱の位置を特定し、図面上でその位置の距離を定規で測ります。
1mmの誤差が誤答につながります。トレーシングペーパーを使って、慎重に作業しましょう。

本問では、8日21時に日本海にある低気圧が、１２時間後の9日9時には道央に移動する予想です（図２）。

以下、8日21時を「移動元」、9日9時を「移動先」と呼びます。

トレーシングペーパーを天気図の上に重ね、移動元の低気圧を取り囲む四隅（緯度・経度の交点）をカギカッコ「」でマーキングします（図３(a)）。×印でマーキングするよりも「」の方が扱いやすいのでおすすめです。

次に、トレーシングペーパーをずらさないように気をつけて、低気圧の上にマーキングします。

通常、低気圧の位置は「L」字の重心にあると言われます。移動計算では移動元と移動先の差分を測るだけなので、「L」字の角にマーキングしました。これでマーキング誤差を減らすことができます。

ちなみにトレーシングペーパーと相性が良いのはシャープペンの芯ですが、色が黒いと天気図の色と重なってしまい視認性が良くありません。マーキングに使用するペンは、赤色のフリクションボールが良さそうです。色鉛筆はトレーシングペーパーとの相性が悪いです。

次に、トレーシングペーパーを移動先の天気図に重ねます。先にマーキングした四隅が一致していることを確認して、移動先のじょう乱をマーキングします。ここでは青色のペンでマーキングしました（図３(b)）。

マーキングが完了したら、赤色と青色のマーキングの間隔（じょう乱の移動距離）を測ります。移動元と移動先の移動距離は、33mmと求まりました（図４(a)）。

 

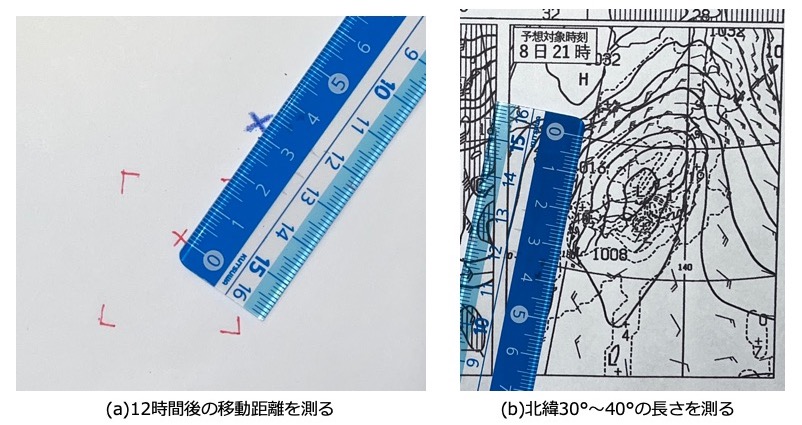
２）経度線を使って移動距離（mm）を「度」に変換する

次に、経度線に沿った１度が何mmになるのかを求めます。

まず、経度線の10度分を測ります。この10度はどこを選んでも良いのではなく、じょう乱が存在する区間を選んでください。

経度線は大円なので北緯30〜40度で測っても、北緯40〜50度で測っても、地球上の距離は同じはずです。しかし天気図は平面なので歪みが生じ、天気図上の長さは異なることになります。

図４(b)ではじょう乱を挟む北緯30〜40度の長さを測ります。北緯30°〜40°の長さ＝35mmとなりました。

35mmが経度10度に相当するので、先に測った33mmは33×10/35＝9.4度になります。

１２時間で9.4度進むということは、１時間で9.4度÷12＝0.78度進むことになります。１ノットは１時間に1/60度進む速さですから、１時間に0.78度進む速さは0.78×60＝46ktになります。５kt刻みでは４５ktになります。

なお、速さを計算するには以下の式を覚えても良いでしょう。

 

 

 

方位を求める

低気圧が8日21時から9日9時までの12時間に進む方向を16方位で答えます。

じょう乱の移動方向を求める問題では、基準となる方角をどこにとるかで答えが異なる可能性があります。

例えば移動元と移動先をつないで南西〜北東の基準線と比べた場合、始点側の赤枠内だけで考えると、移動方向（緑線）は「北北東」と読めなくもありません（図５）。

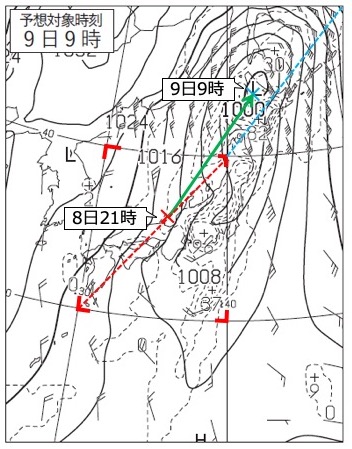
一方で、終点側で方向を読み取ると「北東」と読めます。模範解答は「北東」となっているので、「北北東」は許容範囲ではなさそうです。

先にも記しましたが、天気図の緯度・経度は歪んでいるので、できるだけ長い距離（移動の始点から終点）で比較して判断するのがコツでしょう。

 

最後に

電卓使用を認めない速度計算問題がなぜ頻繁に出題されるのでしょうか。私の邪推ですが、得点を下げるための調整球なのだと思います。

家で問題を解くときには正しく計算できるのに、試験場ではうっかりミスで間違えてしまう。あるいはそもそも計算方法を理解していないなど、正解に達しない原因は様々あるでしょう。いずれにしても、計算問題を出題すると一定数の不正解者が出るのでしょう。

実技試験の趣旨からすれば、すべてを論述形式の出題にするのが望ましいはずです。しかしこれでは採点作業も大変ですし、なかなか得点差がつきにくい場合もあるのではないでしょうか。

そのようなとき、算出結果が一致しなければ間違いと即断できる計算問題の存在意義は大きいのだと思います。

 

この記事が役に立ったと思われた方は、ポチッと押してください。